O módulo 5 “A polarización” é unha das estrelas do kit Photonics Explorer – pola importancia do fenómeno da polarización da luz, polo sinxelo que resulta e tamén porque permite tratar moitos outros aspectos da práctica experimental, como as fontes de erros, a precisión de medidas, ou o concepto de concentración e dilución do azucre.
A polarización é un dos fenómenos tratados nas prácticas recomendadas pola CiUG (Prácticas: Orientacións xerais novo (actualizado a 13/04/2018)), aínda de unha forma diferente. A relación coa práctica da CiUG será tema de outra entrada no blog.
No módulo 5 o alumnado aprenderá a fabricar o seu propio polarímetro e a medir a rotación do plano de polarización cunha solución de azucre. Os detalles veñen explicados no manual do Photonics Explorer. Aquí trataremos algúns detalles prácticos do experimento.
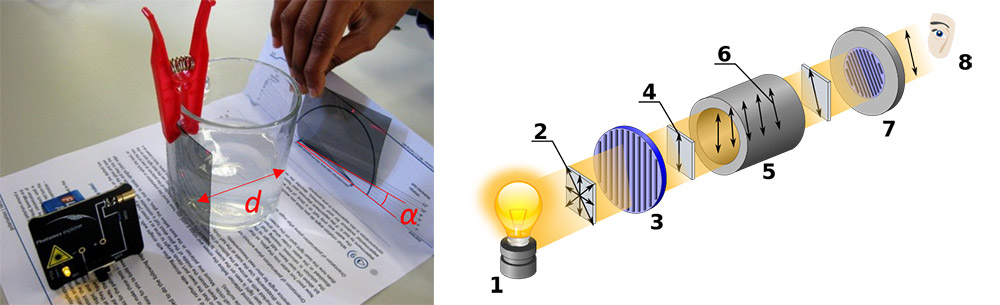
O sentido do xiro – dextroxiro ou levoxiro?
Como nos sinalou o profesor Antón Pérez do IES de Becerreá, nos polarímetros convencionais o observador (8) colócase na posición na que está a pantalla, mirando cara ao láser (1). Unha disolución dextroxira xira entón o plano de polarización ata a dereita (+) (no sentido das agullas do reloxo, ángulo α positivo como na foto) e unha levoxira ata a esquerda (-) con α negativo.
No montaxe do módulo 5 o observador colócase no lado oposto, mirando cara á pantalla coa escala. Desde esa posición as disolucións dextroxiras, que no polarímetro desvían o plano da luz polarizada no sentido das agullas do reloxo, vería que desvían o plano da luz no sentido contrario das agullas do reloxo. Nunha aula suficientemente escura pode ser máis doado observar a intensidade do láser a través do papel, e xirar o analizador ata bloquear a luz do láser.

Na nova versión do WS05.1 ampliamos a escala e corriximos a indicación do sentido do xiro.
Ángulo de rotación
O ángulo de rotación do plano de polarización medido no experimento denominámolo α (“alfa”). Este ángulo experimental depende da concentración de azucre c e da distancia d que percorre a luz polarizada a través da disolución de azucre. Para poder comparar os ángulos de rotación de experimentos con diferentes valores de c e d, definimos o ángulo de rotación específico, ou rotación específica [α], a rotación por cada cm de percorrido e cada kg de azucre por litro de disolución:

O ángulo de rotación α (e [α]) depende ademais da cor da luz utilizada (a súa lonxitude de onda λ) e da temperatura. Ambos os efectos son pequenos e non afectan coa precisión que temos nestas medidas.
Sacarosa, o azucre común
A sacarosa é dextroxira cunha rotación específica [α] = +66,47° dm-1 cm3 g-1. En unidades máis prácticas obtemos [α] = +6,65° cm-1 L kg-1, quere dicir 6,6° por cada centímetro de distancia d percorrida e por cada kg de azucre por litro.
Por exemplo, nun vaso cunha distancia d = 5,0 cm unha disolución de sacarosa de 0,400 kg/L provoca un ángulo de xiro α = +13,3° (= +6,6° cm-1 L kg-1 · 0,400 kg L-1 · 5,0 cm).
Frutosa
A frutosa é levoxira cun ángulo de rotación específico [α] = −92° dm-1 cm3 g-1 = -9,2° cm-1 L kg-1. Este ángulo é negativo e a rotación é oposta á da sacarosa.
Cunha disolución de frutosa de 0,400 kg/L e a unha distancia d = 5,0 cm obtemos un ángulo α = 18,4°( = -9,2° cm-1 L kg-1 · 0,400 kg L-1 · 5,0 cm).
Preparación das disolucións
As cantidades de azucre disoltas son tan grandes que é necesario preparar a disolución en dous pasos.
- Disolve a cantidade necesaria de azucre nun volume de auga menor que o final. Axita e quenta para disolver todo o azucre. Deixa arrefriar.
- Engade auga á disolución para levar o volume ao valor final desexado.
Fontes de erro
É recomendable recoller os resultados dos grupos nunha táboa no encerado e discutir a variación entre os ángulos obtidos.
- Se os alumnos preparan as súas disolucións de azucre entón a concentración c será a fonte de erro principal.
- A distancia d pode variar fortemente dependendo do camiño que percorre a luz na disolución. Se se usan vasos redondos é importante pasar polo centro do vaso.
- A posición do vértice do polarímetro sobre a escala do ángulo é crítica.




